Raza Cercului Inscris In Triunghi Oarecare

Notăm cu r raza cercului înscris în triunghi. Cercul înscris unui triunghi este acel cerc aflat în interiorul triunghiului și căruia toate laturile triunghiului considerate ca segmente și nu prelungirile acestora îi sunt tangente. Triunghi ascuţitunghic toate din unghiurile mai mici de 90.

asrock fm2a55m vg3 compatible processors bahar viata furata ep 1 bine ai venit pe lume ingeras mic asia express sezon 2 online biserica sf nicolae dintr o zi asus ph gtx1050ti 4g benchmark bae suzy dan lee min ho kiss baza 10 in baza 2

Raza Cercului Inscris Si Circumscris Suprafata Triunghiului 7 5 Pg4 Youtube

Cercul Circumscris Triunghiului

3 Centrul Cercului Circumscris Unui Matematica Altfel Facebook

S22 2 Lectie 9a Raza Cercului Circumscris Si Raza Cercului Inscris In Triunghi Tug Of Web

Geometria Plană și In Spațiu

Http Www Mathstrength Com Lectia Geo 9 Cercul Circumscris Triunghiului Youtube

Conform teoremei lui pitagora ac p ab2 bc2 p 252 152 20.

Raza cercului inscris in triunghi oarecare. Ai obținut o formulă a ariei triunghiului funcție de r și perimetrul triunghiului. Inaltimea si mediana triunghiului duse din varful unghiului drept impart acest triunghi in trei. Mai multe informatii se gasesc pe http www prepa ro veti gasi cursuri exemple rezolvate probleme si teste propuse spre rezolvare cuprinzand toata matem. Raza cercului inscris.

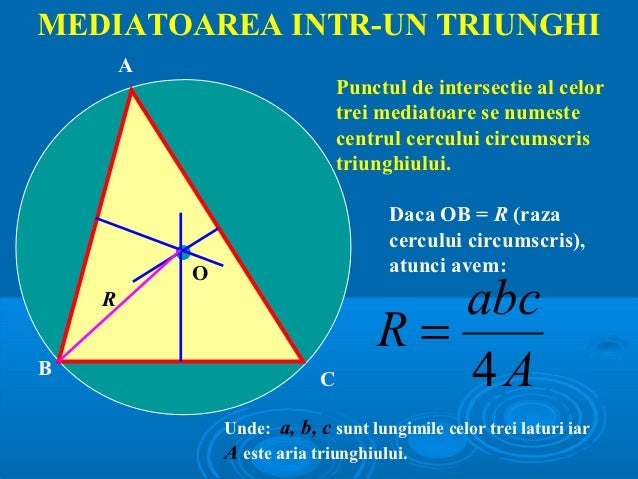
Geometria triunghiului 4 conform teoremei catetei x2 y ab de aici ab x2 y 152 9 25. P a b c 2. Linii importante în triunghi. Raza cercului circumscris triunghiului abc este egală cu.

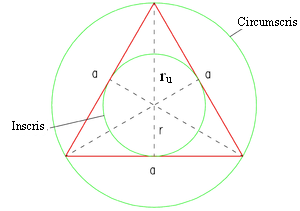
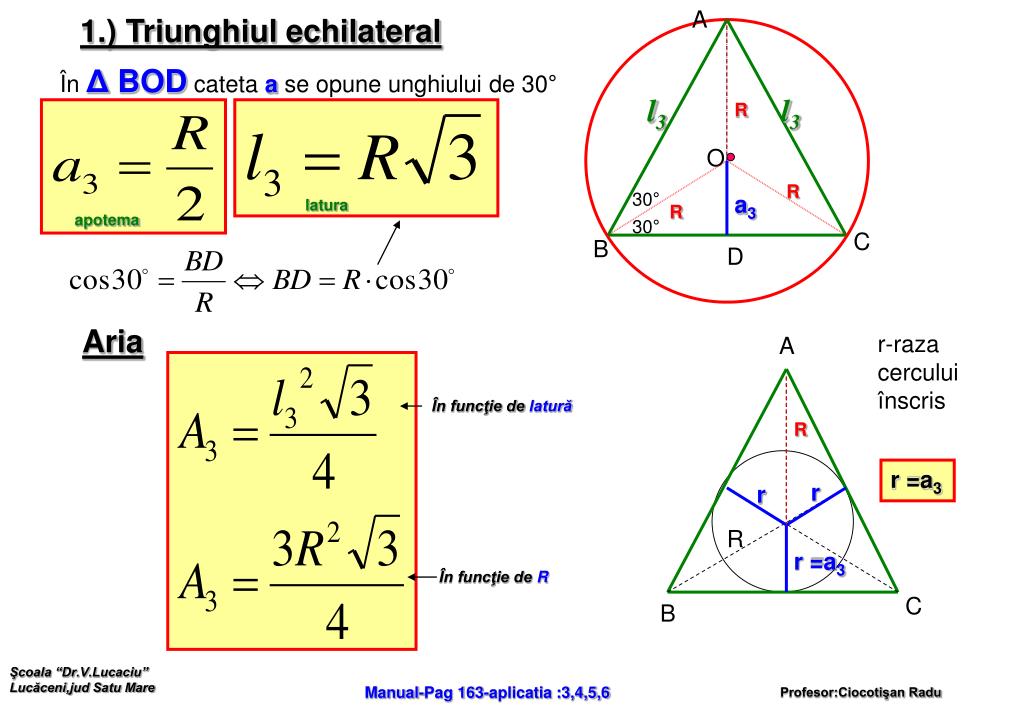
1 bisectoarea este semidreapta care împarte un unghi în două unghiuri congruente sunt concurente în i centrul cercului înscris in triunghi. Exprimă aria triunghiului abc ca sumă a ariilor triunghiurilor notează lungimile laturilor cu a b c. Triunghi scalen sau oarecare are toate cele trei laturi şi unghiuri diferite. Aria unui triunghi poate fi exprimată cu ajutorul mai multor formule unde r este raza cercului circumscris triunghiului abc r este raza cercului inscris in triunghiul abc iar p este semiperimetrul triunghiului.

Cum aflu raza cercului inscris intr un triunghi oarecare in care se cunosc laturile perimetrul si aria. în geometria triunghiului cercul înscris sau exînscris unui triunghi este un cerc tangent tuturor laturilor triunghiului sau prelungirilor acestora. Catetele si ipotenuza unui triunghi dreptunghic au lungimile egale respectiv cu a b si c. R s p unde r raza s aria p perimetrul sau r abc 4s unde a b c sunt lungimile laturilor iar s aria.

Bc 15 cm ac 20 cm ab 25 cm.