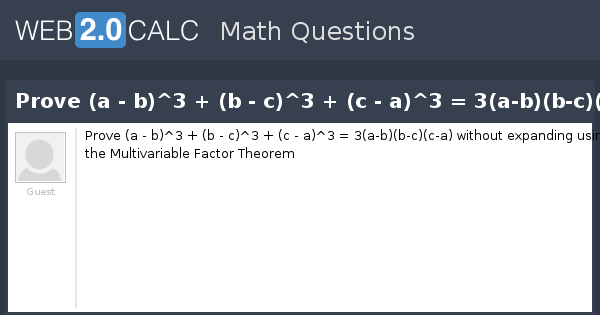
A B 3 B C 3 C A 3 A B B C C A

A 2 ab ac ab b 2 bc ac bc c 2 now combine like words. Asked sep 14 2018 in class ix maths by aditya23 2 145 points polynomials. Factoring by pulling out fails.

hotel transylvania 3 online subtitrat icoana maicii domnului grabnic ajutatoare athos impozite si taxe sector 3 in mintea criminalului film online subtitrat imagini cu povestea ursul pacalit de vulpe if only online subtitrat in romana i mi sau imi imagini de toamna cu ploaie de colorat

Factorise A B 3 B C 3 C A 3 Thanks Math Polynomials 13651723 Meritnation Com

Factorise 2a B C 3 2b C A 3 2c A B 3 Brainly In

Show That A B 3 B C 3 C A 3 3 A B B C C A Brainly In

A B 3 B C 3 C A 3 A A B C A 2 B 2 C 2 Ab Bc Ac B 3 A B B C C A C Youtube

Show That A B 3 B C 3 C A 3 3 A B B C C A Brainly In

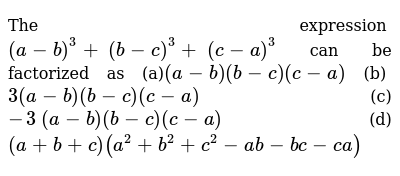
3s Factorise A3 B C 3 B3 C A 3 C3 A B 3 Brainly In

A b c 3 looking for common sub expressions.

A b 3 b c 3 c a 3 a b b c c a. A b 3 b c 3 c a 3 a b b c a b 2 a b b c b c 2 c a 3 a c a 2 2ab b 2 ab b 2 ac bc b 2 2bc c 2 c a 3 c a a 2 3ab 3b 2 ac 3bc c 2 c. To simplify the above expressions start by expanding the binomials. If a b c are all non zero and a b c 0 prove that a2 bc b2 ca c2 ab 3. A c b 3 group 2.

B c a 3 bad news. Note that we can expand the a b 3 b c 3 and c a 3 using the special product formulas for a cube of a binomial. A a a 2 a b ab a c ac b a ab b b b 2 b c bc c a ac c b bc c c c 2 now placed all of them in a row. A b c 3 group 2.

B c a 3 group 3. The groups have no common factor and can not be added up to form a multiplication. Math x y z 0 math hence math x 3 y 3 z 3 3xyz x y z x 2 y 2 z 2 xy xz yz 0 math math x 3. A 3 b a 3 c.

Take each and each huge style interior the 1st set of parentheses and multiply it by applying each thing interior the 2d set. A c b 3 group 3. Let math a b x b c y c a z math it is obvious that.